Introduction
How accurate can you get if you are given a value, say 23.45%, and asked to do certain calculations with it? The answer is that you can only ensure precision up to the amount of precisio that your raw data provided (four digits).
Can you honestly say that the last few decimal places (anything after the first four numbers) imply anynthing meaningful if your answer is anything like 175.8883762 after all of your calculations? Sorry. All of these claims are unsupported and based on your most imprecise measurement.
Significant figures are welcomed in academic circles because they provide you and the reader with a measure of how precise your answer is. A long number may appear cool, but while it is the mathematically “correct” answer, it may be confusing to others down the road.
Significant figures enable you to represent your result in terms of the number of significant digits in your least accurate measured quantity. Accuracy improves with better measurements and, thus, more significant digits.
Definition
“The term significant figures refers to the number of important single digits (0 through 9 inclusive) in the coefficient of an expression in scientific notation. The number of significant figures in an expression indicates the confidence or precision with which an engineer or scientist states a quantity.”
OR
“Significant figures in a place system are numeric numbers that show the precision of the full number.”
OR
“Significant figures are a method of indicating the precision of your numbers in calculations.”
Rules for identifying significant figures
- The significance of all non-zero numbers is taken into account. 38, for example, contains two significant values (3 and 8), whereas 25.31 has four significant figures (2, 5, 3 and 1).
- Locked zeros are significant zeros which occur within two separate digits. 2008, for example, has four significant figures (2, 0, 0, and 8) while 1.0007 has five (1, 0, 0, 0 and 7).
- Opening zeros (zeroes preceding non-zero values) have no significance. 002 has one significant figure (only 2), whereas 0.00014 has two significant figures (1 and 4).
- Trailing zeros (zeroes following non-zero values) in a number without the need for a decimal are often unimportant. For example 5000 has just one significant figure (just 1) and 3200 has two significant figures (3 and 2).
- Trailing zeros (zeroes following non-zero values) in a number with the need for a decimal are often important. For instance, 32.00 has four significant figures (3, 2, 0, and 0), but 54.200 has five (5, 4, 2, 0 and 0).The precision of these figures is clarified by this convention. For example, if a measurement with four decimal places of precision (0.0001) is provided as 12.23, the measurement may be interpreted as having only two decimal places of precision.
- The number 0 has just one meaningful figure. As a result, all zeros after the decimal point are significant as well. For example, the number 0.00 has three significant digits.
- In case of scientific notation all the numbers are significant except powers of 10. For example the number 2.50 × 103 has three significant figures (2, 5 and 0).
How to calculate the problems significant figures?
Example 1:
The distance between moon and sun is 152,503,397 km. determine the number of significant figures.
Step 1: Write the given number
152,503,397 km
Step 2: Using the rule as a guide, identify the number of significant zeros.
Because there is a zero digit between two significant digits in the given number, it is also important. As a result, the number above has one important zero digit.
Step 3: Using the rule as a guide, identify the number of non-zero significant digits.
The above number has eight non-zero significant digits that are 1, 5, 2, 5, 3, 3, 9 and 7.
Step 4: Now add the number of none-zero and zero significant numbers to calculate total number of significant figures.
Since the above number has one zero significant number and eight non-zero significant number that’s why the total number of significant figures in above number are nine (1, 5, 2, 5, 0, 3, 3, 9 and 7). To improve accuracy in the given problem, use the sig fig calculator by following the procedures mentioned below.
Step 1: Put in the number for which you want to calculate significant figures and press the calculate button.
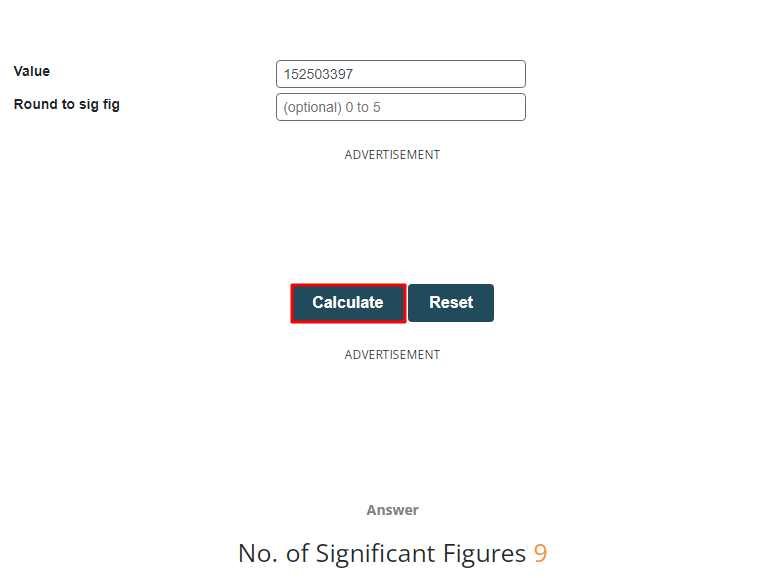
Significant figures have been calculated for you.
Example 2:
The distance between two chemical bonds is 150.00pm. Determine the number of significant figures.
Step 1: Write the given number
150.00pm
Step 2: Using the rule as a guide, identify the number of significant zeros.
It is evident from the number that there are three significant zero digits on the right side of the number.
Step 3: Using the rule as a guide, identify the number of non-zero significant digits.
The above number has two non-zero significant digits that are 1 and 5.
Step 4: Now add the number of none-zero and zero significant numbers to calculate total number of significant figures. Since the above number has three zero significant number and two non-zero significant
number that’s why the total number of significant figures in above number are five (1, 5, 0, 0 and 0).
To find the number of significant figures in the above problem you can use the significant figures calculator by following the below steps.
Step 1: Put in the number for which you want to calculate significant figures and press the calculate button.
Hence the number of significant figures has been calculated.
Summary:
Significant figures enabled scientists to achieve essential accuracy and precision when there was no means to increase accuracy in experimental values or given measurements. Every measurement contains some degree of uncertainty, and significant figures reveal what that uncertainty is.
When performing a computation, your answer can only be as precise as the less precise measurement. Figures of significance propose new methods for determining precision in given numbers and significant figures calculator improves measuring accuracy by one step. It enables user to perform quickly to attain reasonable results.
About The Author
Hemant Singh
Hello friends, I am Hemant, Technical Writer & Co-Founder of Education Learn Academy. Talking about education, I am a student. I enjoy learning things related to new technology and teaching others. I request you that you keep supporting us in this way and we will continue to provide new information for you. :)
Join Telegram:- Click Here