We help you
understand better,
we make it easy.

The Best Educational material at your fingertips, making it more impactful and fun.

Study Material & Live Classes for CBSE, ICSE, NCERT, JEE, NEET & more

LEAD Partner school 1

Study Material & Live Classes for CBSE, ICSE, NCERT, JEE, NEET & more

lpt bg img 2
Homepage 3

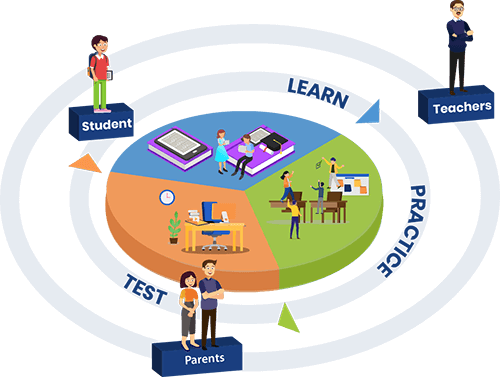
Education Learn Academy Total Learning Ecosystem is a One-App-One-Solution for all stakeholders – Students, Teachers and Parents . It allows students to access learning solutions mapped to their curriculum at home, while simultaneously allowing parents and teachers to track and evaluate the student’s performance.

Highlights –

  • Deep, immersive learning, based on the Learn-Practice-Test pedagogy
  • Promotes independent learning while maintaining continuity from school to home
  • Ensures effective communication between all stakeholders

Extramarks Pedagogy is based on the three-pronged approach of Learn-Practice-Test (LPT)

LEARN | PRACTICE | TEST

NCERT Solutions | RD Sharma Solutions | NCERT Exemplar Problems | CBSE Sample Papers & Mp Board

‏‏‎ ‎‏‏‎ ‎Ncert Solution

View all classes

Mp Board Solution

View all classes

QUICK RESOURCES

Search Any Think

I have made a site for you which covers the Study material. Which is made for the student. You can visit and see. ELA OFFICAL

Our approach to Better Learning

MP Board Books 1 To 12

Rd Sharma Solution

CBSE Sample Papers

Free Cbse Notes Pdf

Reference Book Solutions

USEFUL LINKS

Ncert Books For Class 1 to 12

State-Wise School Books 1-12 Classes Online For Free

Textbook Solutions is Updated

Recent Post